Real Estate Math Formulas, Practice Questions, & Examples

Real Estate Math Formulas, Practice Questions, & Examples
For some people, math can be intimidating. While you might think you can avoid the subject when working in real estate, there’s actually a lot of math you’ll use in your day-to-day life as an agent. There will also be a few math questions on your real estate exam.
Below, we've put together a partial study guide for real estate math that includes formulas, practice questions and answers, as well as examples you might see on your exam or in your career as a real estate agent.
How Much Math Is on the Real Estate Exam?
No matter what state you're in, earning your real estate license will require correctly answering math questions on the licensing exam. The exact number of math questions will vary from state to state, but generally, math-related questions make up 10-15% of the test.
Is Real Estate Math Difficult?
Many students dread the idea of learning and using math for their careers. The good news is that real estate math is NOT difficult.
There are two reasons you need to practice real estate math now:
- You'll encounter math problems on the licensing exam, as explained above.
- Learning and working on these math problems will help you understand financial and spatial concepts that you will encounter in your career.
Once you're licensed, you probably won't use real estate math every day. When it does come up, you'll be able to look up concepts and formulas as you need to. However, practicing now will help cement those ideas.
How Is Math Used in Real Estate?
Real estate math is mostly focused on calculating the size of various spaces and the economics of real estate transactions.
Math concepts that real estate agents need to know will include:
- Measurement Conversions, including those related to area measurements, linear measurements, and volume measurements.
- Fractions, Decimals, and Percentages, including how to solve percentage problems and how to use the T-Bar Method.
- Real Estate Math Formulas related to problems you'll encounter frequently as an agent. These include the Gross Rent Multiplier (GRM) Formula, the Commission Formula, the Simple Interest Formula, the Loan Value Ratio (LTV), and more.
Real Estate Math Definitions
You'll need to learn many basic math definitions for your real estate exam, but the most unfamiliar ones are typically the terms that relate to real estate surveying. Here are a few examples:
| Term | Definition |
|---|---|
| Baseline | A measured line through a survey area from which triangulations are made |
| Benchmark | A surveyor's mark is made on a stationary object of previously determined position and elevation and used as a reference point in tidal observations and surveys. |
| Board Foot | A unit of cubic measure for lumber. Equal to one foot square by one inch thick. |
| Front Foot | A method of describing or pricing commercial real estate by the number of feet of road frontage the parcel has. The drawback is that there is no widely recognized standard for depth, so a property selling for $1,500 per front foot might be half the depth of one selling for $2,400 a front foot, but no one can tell just from the price. |
| Governmental Survey System/Rectangular Survey System: | A system of dividing land in the United States into 24-square mile quadrangles from the north-south line and the east-west line. |
| Latitude | The angular distance north or south of the earth's equator, measured in degrees along a meridian, as on a map or globe. |
| Longitude | Angular distance on the earth's surface, measured east or west from the prime meridian at Greenwich, England, to the meridian passing through a position, expressed in degrees (or hours), minutes, and seconds. |
| Meridian | An imaginary great circle on the earth's surface that passes through the North and South geographic poles. All points on the same meridian have the same longitude. |
| Point of Beginning | The point of beginning is a surveyor's mark at the beginning location for the wide-scale surveying of land. |
| Range | A north-south strip of townships, each six miles square, numbered east and west from a specified meridian in a U.S. public land survey. |
| Running Foot | A measurement of the length of a piece of wood, without regard to its thickness or width. |
| Township | A public land surveying unit of 36 sections or 36 square miles. |
View more basic real estate math definitions inside our Principles in Real Estate course.
Measurement Conversions
On the real estate licensing exam, you may be asked to do math problems where you need to convert between different units of measurement to get the size of a space.
You'll need to know how to convert between different units for linear, area, and volume measurements.
Let's go through each type of measurement conversion and the units you'll need to know. Then, we'll provide an example problem you might see on the exam and show you how to complete it.
Linear Measurements & Conversions
When you measure length, width, or height, you may need the following conversions.
- 1 foot = 12 inches
- 1 yard = 3 feet
- 1 mile = 5,280 feet
In real estate, you also need to understand survey measurement units (links, rods, chains), which are archaic. You need to know how these terms relate to each other:
- 1 rod = 25 links
- 1 chain = 4 rods
You also need to know how to convert these archaic units into more conventional linear units.
- 1 link = 7.92 inches
- 1 rod = 16.5 feet
- 1 mile = 320 rods
Area Measurements & Conversions
When you're calculating the area of a space, you may need to know the following conversions.
- 1 square foot = 144 inches
- # square inches ÷ 144 = # square feet
- # square feet × 144 = # square inches
- 1 square yard = 1,296 square inches
- # square inches ÷ 1,296 = # square yards
- # square yards × 1,296 = # square inches
- 1 square yard = 9 square feet
- # square feet ÷ 9 = # square yards
- # square yards × 9 = # square feet
- 1 acre = 43,560 square feet
- # square feet ÷ 43,560 = # acres
- # acres × 43,560 = # square feet
- 1 section = 1 square mile
- 1 section = 640 acres
- # acres ÷ 640 = # sections (or square miles)
- # sections (or square miles) × 640 = # acres
- 1 hectare = 2.471 acres
- # hectares ÷ 2.471 = # acres
- # acres x 2.471 = # hectares
- 1 township = 36 sections
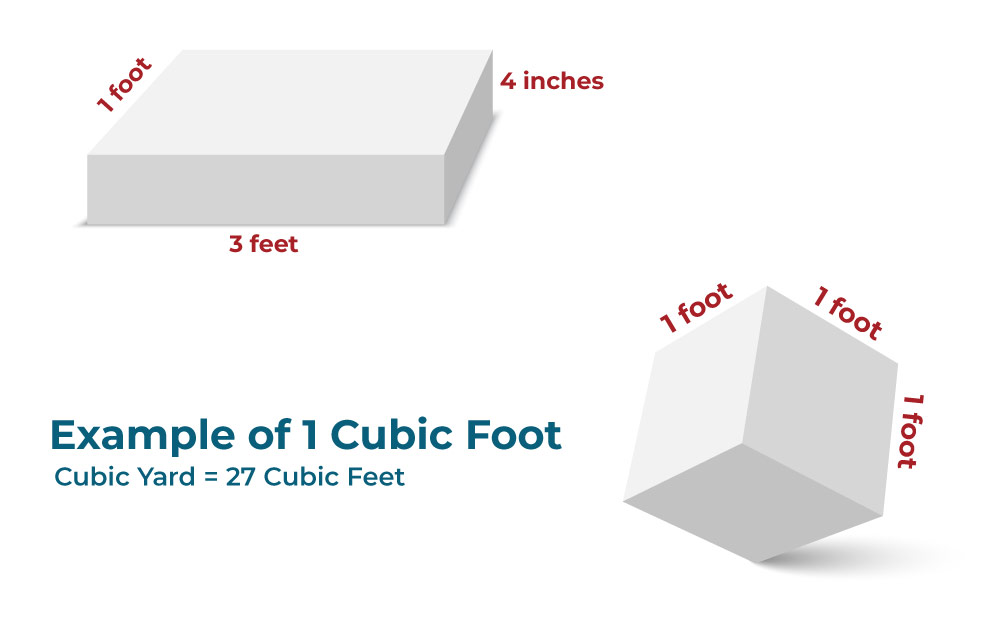
Volume Measurements & Conversions
To calculate the volume of a space, you may need to know the following conversions.
- 1 cubic foot = 1,728 cubic inches
- # cubic inches ÷ 1,728 = # cubic feet
- # cubic feet × 1,728 = # cubic inches
Example Measurement Conversion Problem
Your client needs to rent climate-controlled, insured, and bonded warehouse space for six months to store 500 pallets of construction tools from the largest toolmaker in China, each full pallet being 4 feet by 5 feet by 8 feet tall, and all shrink-wrapped in industrial-grade plastic. The only space that's available in town leases for 22.5 cents/cubic foot/month. What is the cost of the space?
Step 1: 4 feet × 5 feet × 8 feet = 160 cubic feet per pallet
Step 2: 160 cubic feet x 500 pallets = 80,000 cubic feet
Step 3: 80,000 cubic feet × $.225/cubic foot/month = $18,000/month
Step 4: $18,000/month × 6 months =
Answer: $90,000 total cost
Fractions, Decimals, and Percentages
Related Terms
| Term | Definition |
|---|---|
| Decimal | A fraction expressed pertaining to tenths or the number 10. The symbol that creates a decimal is called the decimal point. In the number 125.67, the period between the 5 and the 6 is called the decimal point. |
| Denominator | The top number in a fraction that represents how many equal parts one item is divided into. |
| Equivalent Fraction | Fractions which have the same value, even though they may look different. For example, 1/2 and 2/4 are equivalent because they are both halves. |
| Fraction | An expression that indicates the quotient of two quantities, such as 1/3 A disconnected piece; a fragment. |
| Greatest Common Factor | The largest whole number that divides evenly into each of the numbers. For example, the greatest common factor of 4, 8, 12, and 16 is 4 because 4 is the largest number that will divide evenly into each of the numbers. 4÷4=1, 8÷4=2, 12÷4=3, 16÷4=4. |
| Lowest Common Denominator | In mathematics, the lowest common denominator or least common denominator (abbreviated LCD) is the least common multiple of the denominators of a set of fractions. It simplifies adding, subtracting, and comparing fractions. |
| Numerator | The top number in a fraction. Represents how many parts are being counted. |
Fractions
A fraction is a part of a whole item. Fractions tell us how many parts the whole is divided into, as well as how many of those parts we are working with.
For example, in the fraction ¼, the bottom number tells us the item has been divided into 4 parts. The top number, the numerator, tells us we are working with 1 of those 4 parts.
Decimals
Fractions can also be expressed as decimals.
How do you convert a fraction to a decimal? Simply by dividing the top number (numerator) by the bottom number (denominator).
For example, you'd convert ¾ to the equivalent decimal by diving three by four: 3 ÷ 4 = .75
On your real estate licensing exam, you'll be allowed to use a calculator. Calculators use decimal points rather than fractions. In other words, you can enter 1.25 on the calculator; you cannot enter 1 ¼. As a result, it's best to convert any fractions from a problem into decimals before you start other calculations.
Percentages
A percentage is an expression meaning "per hundred" or "per hundred parts." If you say "3%," you are saying that the item being measured has been divided into 100 parts and that the portion you are describing is made up of three of those 100 parts.
It's easy to convert percentages to decimals when you remember this definition. Just use the percentage as the numerator and 100 as the denominator. 23% = 23/100
To convert percentages directly to decimals, move the decimal point two places to the left. To convert decimals to percentages, move it to the right. Use placeholder zeros when necessary to "see" the decimal:
- 10.0% = .10 (decimal two places to the left)
- .01 = 01.0% (decimal two places to the right)
Solving Percentage Problems
There are three formulas that are important for solving all percentage problems.
- PART = TOTAL × RATE
- TOTAL = PART ÷ RATE
- RATE = PART ÷ TOTAL
Another way to remember these formulas is to think:
- If PART is unknown, then multiply the two known numbers.
- If PART is known, then divide.
- When you divide, always enter PART into the calculator first.
T-Bar Method
Many real estate students do not feel comfortable with the 3 formulas used to solve percentage problems, so another way to approach this is to visualize a 'T.' The 'T' will represent the relationship between PART, TOTAL, and RATE. This method is known as the T-Bar Method.
To use the T-Bar method:
- Insert the known figures in the correct places inside the circle (as pictured below).
- If the line between the figures is vertical, multiply to get the unknown.
- If the line between the figures is horizontal, divide to get the unknown. When dividing, always input PART first into the calculator.
Real Estate Math Formulas
Memorizing math formulas is essential for successfully passing your licensing exam. Practice makes perfect, so the more time you spend memorizing these formulas, the better off you will be.
Here are some of the formulas you'll need to memorize.
Loan to Value (LTV) Ratio
Formula:
LTV Ratio = APV ÷ MA
Terms:
- LTV Ratio = Loan to Value Ratio
- APV = Appraised Property Value
MA = Mortgage Amount
Simple Interest Formula
Formula:
A = P(1 + rt)
Terms:
- A = Total Accrued Amount (principal + interest)
- P = Principal Amount
- I = Interest Amount
- r = Rate of Interest per year in decimal; r = R/100
- R = Rate of Interest per year as a percent; R = r * 100
- t = Time Period involved in months or years
Gross Rent Multiplier
Formulas:
- Gross Rent Multiplier = Property Price ÷ Gross Annual Rental Income
- Annual Gross Rental Income = Monthly Rental Income × 12
Property Tax Formulas
Property taxes are typically calculated by multiplying the assessed value of the home by the local "mill rate" ($1 tax for every $1,000 of assessed value).
Formulas:
- Property Tax Rate = Assessed Value × Mill Rate
- Assessed Value = Assessment Market × Market Value
Discount Points Formulas
A discount point or mortgage point is an up-front fee that lowers the interest rate on a home loan. One discount point costs 1% of your total home loan amount. In other words, discount points are basically prepaid interest.
Formula:
Break-Even Point = Points Cost ÷ Monthly Payment Savings
"The Mortgage Rule of Thumb" (28/36 Rule) Formula
Housing Costs to Qualify for Most Loans = Gross Monthly or Annual Income × .28
Proration
The proration process is used to determine the fair division of the costs and benefits of a financial transaction.
At closing, various items are prorated, and some fees are shared among the buyer, seller, and brokers. In other words, the total amount must be prorated or allocated according to a proportionate distribution. Typical expense items to be prorated include property taxes, monthly interest due when loans are assumed, rent, and homeowner fees.
Prorating Interest on Loans
Interest is almost always paid in arrears (at the end of the period). When you make your mortgage payment on the first of the month, you are paying the interest for the previous month.
Interest on a new loan is calculated as follows:
Total Interest = (Principal Balance x Interest Rate) ÷ 365 days of the year
Prorating Loan Interest Example Problem
The Buyer obtains a new loan in the amount of $150,000.00 at 8% interest. The closing is to take place on July 15. How much interest will the buyer pay for July?
Step 1: $150,000.00 x .08 = $12,000.00 in interest
Step 2: $12,000.00 ÷ 365 days a year = $32.876712 per day (per diem)
Step 3: 31 days in July – 14 days before purchase = property owned for 17 days in July
Step 4: $32.876712/day x 17 days = $558.904104
Answer: $558.90 interest in July
Now It's Time to Start Practicing
In this post, we covered a variety of real estate math topics, math formulas, and basic arithmetic skills that you’ll need to know to pass the real estate exam and have a successful career.
You can also find additional practice questions and problems in our real estate exam prep courses and with flashcards to help you study. Ready to get your real estate license? Head to our website and choose your state to get started.